LeetCode 832: Flipping An Image

The Problem

image flip
image flip
  1. Problem Breakdown
    1. Reversing An Array
    2. Inverting A Bit
    3. Inverting An Array
    4. Naive Solution Code
  2. Iterating On Our Solution
    1. Better Solution Code
  3. Iterating On Our Solution Some More
    1. Even Better Solution Code
  4. Algorithmic Complexity
  5. In Conclusion

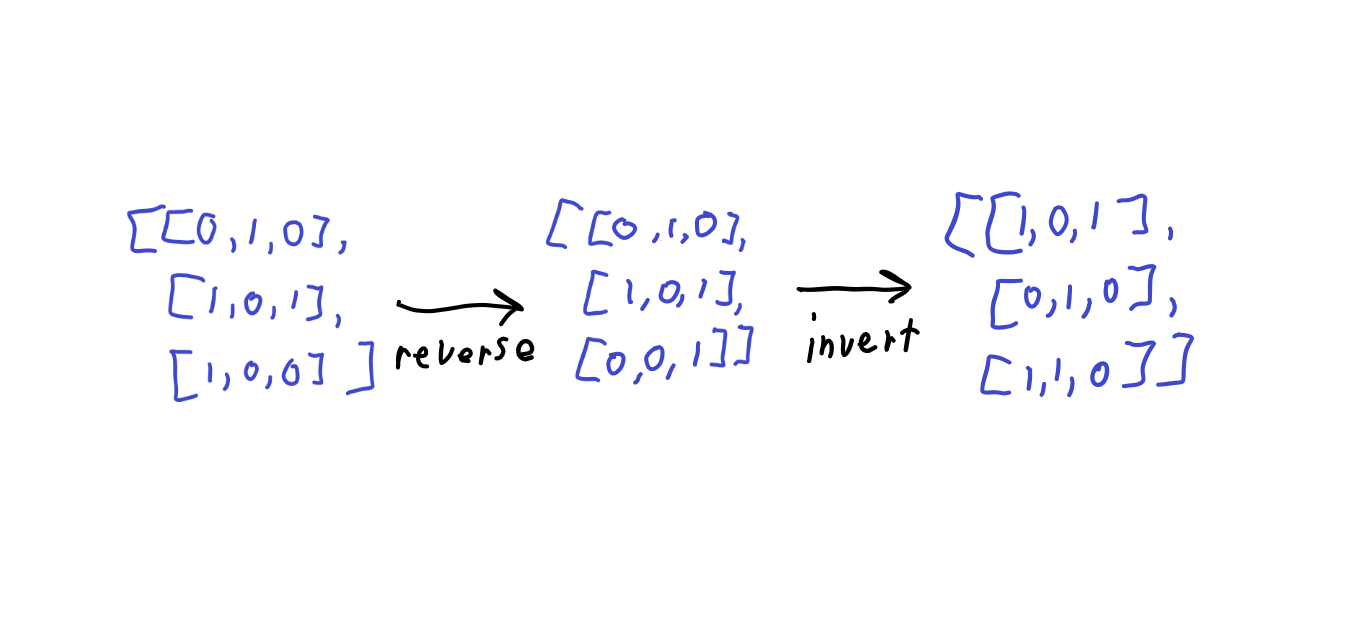
Problem Breakdown

This problem can be broken down into roughly three parts. Reversing an array, inverting a single bit, and inverting an array of bits.

Reversing An Array

To reverse an array in JavaScript, the simplest thing we can do is to use a placeholder array. To do so we will create a new empty array which we will call arrayX, iterate over our input array - arrayY - and add the elements to arrayX in reverse order as we go.

In JavaScript, it is easy to add elements to the end of an array using Array.push(). That means if we iterate over arrayX backwards, we can easily push each element to the end of arrayY and we will have our reversed array.

At this point, we have two options - we can return arrayY (which if you were coding for production you would probably want to do), or we can somehow make arrayX become arrayY. With our current implementation, neither of these choices provides noticeable benefits over the other. However, you will notice that for each array, we will need 2n memory - where n is the number of elements in the array - to hold both arrayX and arrayY. At this point we also think that we can come up with a better solution later where we rearrange arrayX "in place" and only need n memory. For that reason, we will turn set arrayX = arrayY at this point and the function will return void.

If you try this, you will notice a problem. This function will run, but back in the calling context, arrayX will remain unchanged. This is because JavaScript handles certain kinds of function parameters in kind of an interesting way. For objects and arrays, the reference to the original object or array is immutable. We can change what the symbol points to withinin the function scope because JavaScript is a dynamic language and pretty much anything goes. However, that change will not be persisted outside the scope of that function. The weird thing is - we can change the members of that object or array and those changes will be persisted outside of the scope of the function.

The following code will demonstrate this point better than I can with words.

function changeArrayReference(array) {
  const arr = [1, 2];
  array = arr;
}


function changeArrayElements(array) {
  array[0] = 1;
  array[1] = 2;
}


let array = [5, 6];
changeArrayReference(array);
console.log("After calling changeArrayReference(): array ==", array);
changeArrayElements(array);
console.log("After calling changeArrayElements(): array ==", array);

Output:

After calling changeArrayReference(): array == [ 5, 6 ]

After calling changeArrayElements(): array == [ 1, 2 ]

Because of this interesting behavior, once we have set arrayY up how we need it, we will have to iterate over arrayX and set its elements equal to the corresponding element of arrayY one at a time. For now this means we will have to iterate over this array twice. If you're keeping score we're currently using 2n memory and 2n operations. Our algorithmic complexity is weeping.

/**
 * @param {Array<0 | 1>} arrayX
 */
function reverseArrayOfBitsInPlace(arrayX) {
  const arrayXLength = arrayX.length;
  let arrayY = [];
  for (let i = arrayXLength - 1; i >= 0; i--) {
    arrayY.push(arrayX[i]);
  }


  for (let i = arrayXLength - 1; i >= 0; i--) {
    arrayX[i] = arrayY[i];
  }
}

Inverting A Bit

Alright enough of that tricky business, let's talk about something simple. Calling the ! operator on a number in JavaScript will coerce the value into a boolean. That means we're going to have to use an if statement (or a ternary) to return a 0 if the bit is 1 and a 1 if the bit is 0. Simple stuff.

/**
 * @param {0 | 1} bit
 * @return { 0 | 1}
 */
function getBitInverse(bit) {
  if (bit === 0) {
    return 1;
  } else {
    return 0;
  }
}

Inverting An Array

If we can invert a bit and loop over an array, we can invert an array of bits. Luckily, this won't have the same 2-pass property as our reverse logic above.

/**
 * @param {Array<0 | 1>} bitArray
 */
function invertArrayOfBitsInPlace(bitArray) {
  const bitArrayLength = bitArray.length;
  for (let i = 0; i < bitArrayLength; i++) {
    bitArray[i] = getBitInverse(bitArray[i]);
  }
}

Naive Solution Code (3-pass)

Alright now, let's put it all together. We just have to call our reverse logic on each array of the image array, then our invert logic and we're golden. This solution works, but it's a huge bummer. First off, using 3 passes for each array of the image array, it's about average speed for a JavaScript program on leetcode. Second, it uses a ton of space having to create what are essentially 2 copies of each array in the image array. The good news is - we have a working solution, and now we know where we can improve.

/**
 * @param {Array<Array<0 | 1>>} image
 * @return {Array<Array<0 | 1>>}
 */
function flipAndInvertImage(image) {
  const imageLength = image.length;


  for (let i = 0; i < imageLength; i++) {
    reverseArrayOfBitsInPlace(image[i]);
  }


  for (let i = 0; i < imageLength; i++) {
    invertArrayOfBitsInPlace(image[i]);
  }
  return image;
}


/**
 * @param {Array<0 | 1>} arrayX
 */
function reverseArrayOfBitsInPlace(arrayX) {
  const arrayXLength = arrayX.length;
  let arrayY = [];
  for (let i = arrayXLength - 1; i >= 0; i--) {
    arrayY.push(arrayX[i]);
  }


  for (let i = arrayXLength - 1; i >= 0; i--) {
    arrayX[i] = arrayY[i];
  }
}


/**
 * @param {Array<0 | 1>} bitArray
 */
function invertArrayOfBitsInPlace(bitArray) {
  const bitArrayLength = bitArray.length;
  for (let i = 0; i < bitArrayLength; i++) {
    bitArray[i] = getBitInverse(bitArray[i]);
  }
}


/**
 * @param {0 | 1} bit
 * @return { 0 | 1}
 */
function getBitInverse(bit) {
  if (bit === 0) {
    return 1;
  } else {
    return 0;
  }
}

Iterating On Our Solution

Although the problem specifies that we have to reverse the bits in the array, and then invert them, it doesn't actually seem to care that it happens in that order. The only thing it's concerned with is the expected input gives the expected output. This is good news for us because it means we can invert the bits while we're reversing.

In fact, we can get rid of the invertArrayOfBitsInPlace function entirely. Now we can simply call the getBitInverse function on each element of the array as we assign them from arrayY to arrayX.

This algorithm has much better complexity properties. It uses only 2n memory and 2n operations compared to 3n with the above algorithm. Ya ya, it's all O(n), but 1/3 better is 1/3 better.

Better Solution Code (2-pass)

/**
 * @param {Array<Array<0 | 1>>} image
 * @return {Array<Array<0 | 1>>}
 */
function flipAndInvertImage(image) {
  const imageLength = image.length;


  for (let i = 0; i < imageLength; i++) {
    reverseAndInvertArrayOfBitsInPlace(image[i]);
  }


  return image;
}


/**
 * @param {Array<0 | 1>} arrayX
 */
function reverseArrayOfBitsInPlace(arrayX) {
  const arrayXLength = arrayX.length;
  let arrayY = [];
  for (let i = arrayXLength - 1; i >= 0; i--) {
    arrayY.push(arrayX[i]);
  }


  for (let i = arrayXLength - 1; i >= 0; i--) {
    arrayX[i] = getBitInverse(arrayY[i]);
  }
}


/**
 * @param {0 | 1} bit
 * @return { 0 | 1}
 */
function getBitInverse(bit) {
  if (bit === 0) {
    return 1;
  } else {
    return 0;
  }
}

Iterating On Our Solution Some More

You'll remember earlier we talked about reversing arrayX "in place". Here we finally get to the nitty-gritty. You may remember a certain introduction to programming course. Maybe it was at a university, maybe a bootcamp - maybe it was online. In that course you will almost certainly have had to swap two variables using a third variable. We can use that same concept to swap all the variables of our array, in place, starting from the ends and working toward the middle. If you swap array[0] with array[array.length - 1], then swap array[1] with array[array.length - 2] and so on, by the time you reach the middle element, you will have reversed the whole array.

In this case we'll use two "third variables" to keep things simple but come to think of it, you could probably get away with only using one.

Even Better Solution Code (1-pass)

/**
 * @param {Array<Array<0 | 1>>} image
 * @return {Array<Array<0 | 1>>}
 */
function flipAndInvertImage(image) {
  const imageLength = image.length;


  for (let i = 0; i < imageLength; i++) {
    reverseAndInvertArrayOfBitsInPlace(image[i]);
  }


  return image;
}


/**
 * @param {Array<0 | 1>} arrayX
 */
function reverseAndInvertArrayOfBitsInPlace(arrayX) {
  const arrayXLength = arrayX.length;


  let startContainer;
  let endContainer;


  for (let i = 0, j = arrayXLength - 1; i <= j; i++, j--) {
    startContainer = arrayX[i];
    endContainer = arrayX[j];
    arrayX[i] = getBitInverse(endContainer);
    arrayX[j] = getBitInverse(startContainer);
  }
}


/**
 * @param {0 | 1} bit
 * @return { 0 | 1}
 */
function getBitInverse(bit) {
  if (bit === 0) {
    return 1;
  } else {
    return 0;
  }
}

Algorithmic Complexity

Finally, we've converged on a very nice solution. We're using n operations and n memory - 1/3 of our initial implementation. Yes, it's been O(n) the whole time, but now our solution is looking a lot better than average on leetcode.

In Conclusion

The takeaway here is to start with a simple, naive implementation, and iterate on it until we have something we're happy with. The 1-pass solution would have been tricky to come up with if we didn't already have a solid base. Trying to solve too many problems at once will leave you confused and frustrated. Engineering is the process of breaking down problems into smaller, simpler pieces.